FIFA Online 3 强化概率模型推导

今年4月24日，腾讯游戏公布了 FIFA Online 3 的强化概率（原文链接）。这份公式首先写的十分晦涩，总结下来已经公布的强化概率如下表所示:

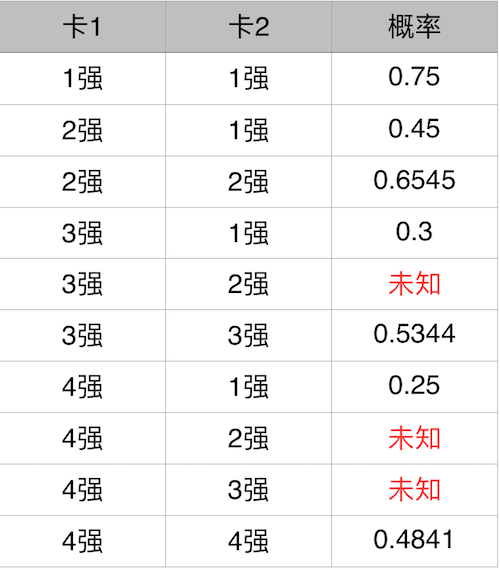
其次，不知是出于什么目的，腾讯没有公布3+2，4+2，4+3，以及5强以上的所有强化概率，因此本文将首先探讨这个游戏背后的强化概率模型，并对5强以上的强化概率进行预测。

计算原理

首先，我们提出一个假设，叫做“成本等价”，即“得到1张高强卡所需消耗的1强卡数量期望与强化路径无关”。举个例子，假如我们有1000张1强卡，想全部强化成3强卡，那么有两种强化路径，一是先全部合成2强卡，再由2强卡与2强卡强化得到3强卡；二是先部分强化成2强卡，然后将2强卡与1强卡强化得到3强卡。分别计算这两种方式：

路径1

将1强卡全部强化为2强，强化500次，成功概率是0.75，可以得到375张2强卡；将2强卡全部强化为3强，强化187.5次，成功概率0.6545，可以得到122.71875张3强卡

路径2

将727.27272张1强卡强化为2强，强化363.36363次，成功概率0.75，得到272.72727张2强卡，将这些2强卡与剩下的272.72727张1强卡强化，成功概率0.45，得到122.727张3强卡

可以看到，两种强化方式最终得到的3强卡数量都约等于122.72张（其实严格相等，误差来自于2+2成功概率的不精确），即每得到一张3强卡，大约需要消耗8.15张1强卡，即所谓的成本等价。

1-5强概率计算

在“成本等价”的前提下，只需已知N强卡与1强卡强化的成功概率，就可以计算出N强卡与1~N-1强卡强化的成功概率。

用 $ P(n,k),1 \le k \lt n $ 表示$ n $强卡与$ k $强卡强化的成功概率，用 $ f(n) $ 表示得到一张n强卡需要消耗的1强卡数量，已知

$$ \begin{cases} P(1,1)=0.75 \\ P(2,1)=0.45 \\ P(3,1)=0.3 \\ P(4,1)=0.25 \\ f(1)=1 \end{cases} $$

假设使用一张 n-1强卡与一张k强卡强化，有$ P(n-1,k) $的概率强化成功，此时消耗了$ f(n-1)+f(k) $张1强卡；有$ 1-P(n-1,k) $的概率强化失败，此时已经消耗了$ f(n-1)+f(k) $张1强卡，但是因为强化失败，为了得到 n 强卡，还需要$ f(n) $张1强卡。故有

$$ f(n)=P(n-1,k) \times (f(n-1) + f(k)) + (1-P(n-1,k)) \times (f(n-1)+f(k)+f(n)) $$

即

$$ f(n)=f(n-1)+f(k)+(1-P(n-1,k))\times f(n) $$

即

$$ f(n)={f(n-1)+f(k) \over P(n-1,k)} $$

计算得

$$ \begin{cases} f(2)={8 \over 3} \\ f(3)={220 \over 27} \\ f(4)={2470 \over 81} \\ f(5)={10204 \over 81} \\ \end{cases} $$

以及

$$ \begin{cases} P(2,2)={36 \over 55} \approx 0.6545 \\ P(3,2)={438 \over 1235} \approx 0.3547 \\ P(3,3)={132 \over 247} \approx 0.5344 \\ P(4,2)={1343 \over 5102} \approx 0.2632 \\ P(4,3)={1565\over 5102} \approx 0.3067 \\ P(4,4)={1235\over 2551} \approx 0.4841 \\ \end{cases} $$

至此我们计算出了所有5强以内的强化概率

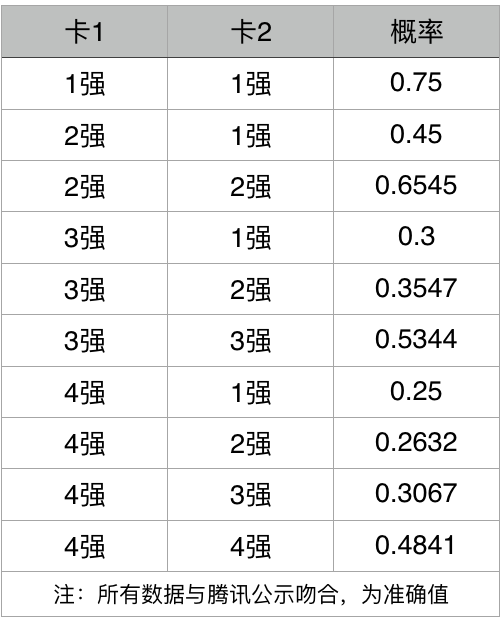
6-10强概率估测

如上文所示，任意强卡与1强卡的强化成功率是游戏运营人员配置，这是不难解释为什么1+1，2+1，3+1，4+1分别是75%，45%，30%，25%这类整数值，而其余概率则根据“成本等价”原则计算。 因为腾讯没有公布5+1,6+1,7+1,8+1,9+1的概率，这部分内容只能是本人的一些预测。 显然随着强化等级的提高，与1强卡强化的成功率呈下降趋势，将已有的数据使用乘幂曲线拟合

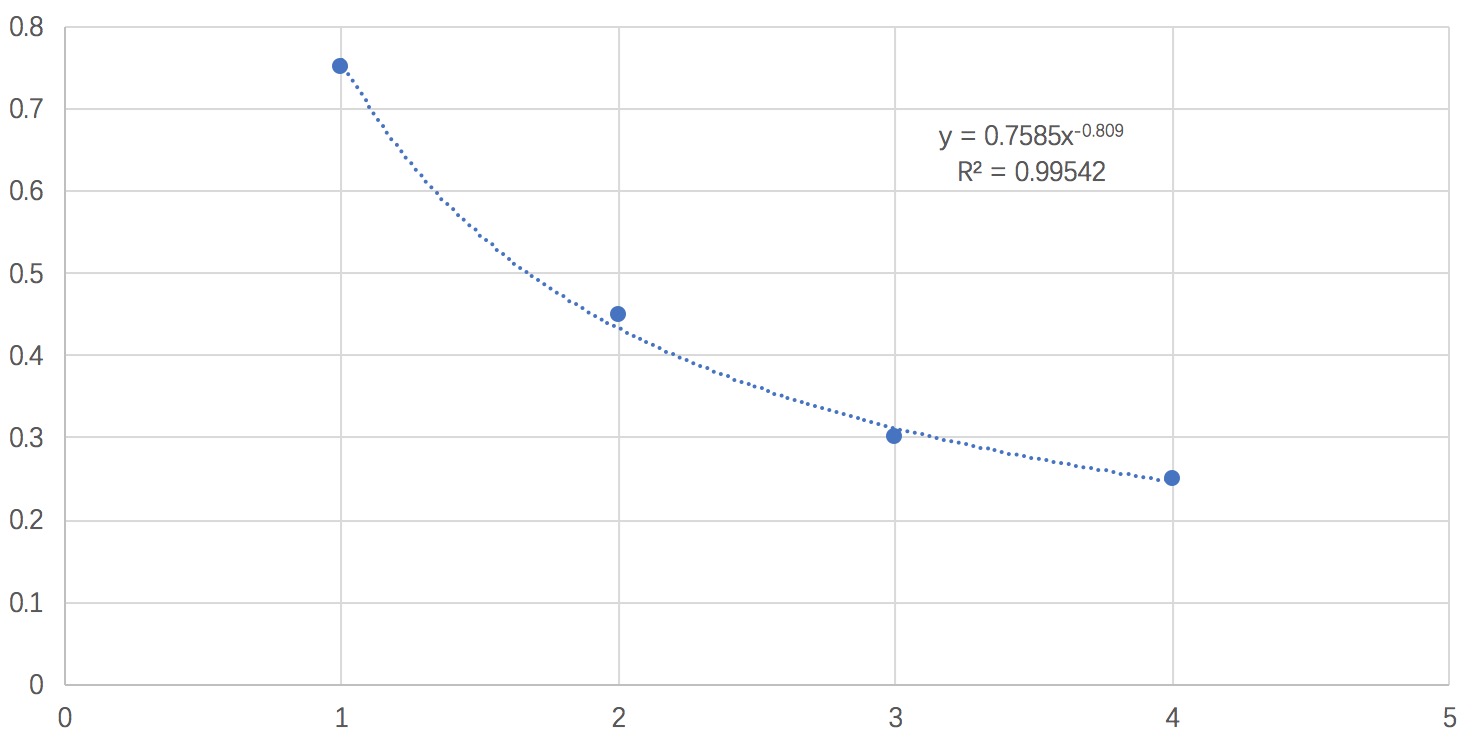
由此对5~9强卡与1强卡的强化概率进行估算，进一步估算出所有的强化概率

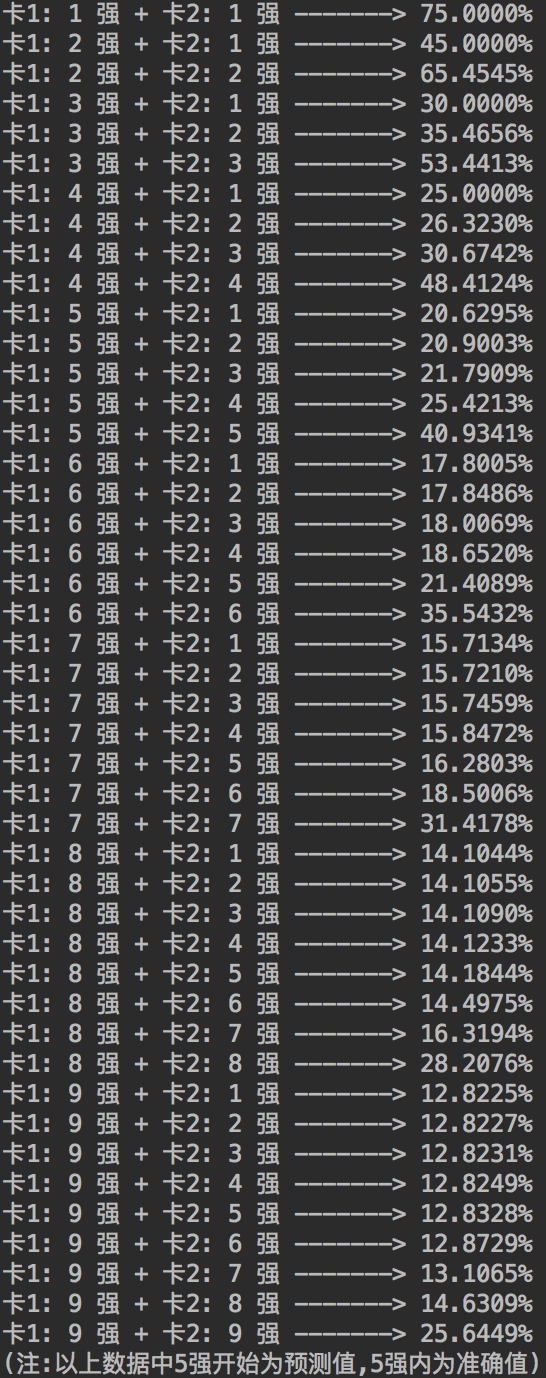
附1

概率计算源码

public class Fifaol3 {
    private static double[][] P = new double[10][10];
    private static double[] f = new double[11];
    private static void init_P() {
        P[1][1] = 0.75;
        P[2][1] = 0.45;
        P[3][1] = 0.3;
        P[4][1] = 0.25;
    }
    private static void init_f() {
        f[1] = 1;
    }

    private static void calc_P() {
        for (int i = 5; i <= 9; i++) {
            P[i][1] = 0.7585 * Math.pow(i, -0.809);
        }
    }

    private static void calc_f() {
        for (int i = 2; i <= 10; i++) {
            f[i] = (f[i - 1] + f[1]) / P[i-1][1];
        }
    }

    public static void main(String[] args) {
        init_P();
        init_f();
        calc_P();
        calc_f();
        for (int i = 1; i <= 9; i++) {
            for (int j = 1; j <= i; j++) {
                if (j > 1) {P[i][j] = (f[i] + f[j])/ f[i + 1] ;}
                System.out.println(String.format("卡1: %d 强 + 卡2: %d 强 -------> %.4f%%", i, j, P[i][j] * 100));
            }
        }
        System.out.println("(注:以上数据中5强开始为预测值,5强内为准确值)");
    }
}

附2

不负责任的猜测：腾讯的公示为什么写的这么晦涩，为什么不公布其余强化的概率？因为按照“成本等价”计算，高强中卡等级的提升对成功概率的提升非常微弱，例如7+1到7+4的成功概率几乎是一样的。