落单的数是一道很有趣的算法题，题目如下

给出2*n + 1 个的数字，除其中一个数字之外其他每个数字均出现两次，找到这个数字。

$ O(N^2) $ 的解法是显而易见的，如果加上时间复杂度 $ O(N) $ 的限制，问题就有些麻烦，好在我们可以使用HashMap来满足要求，但再加上空间复杂度$ O(1) $ 的要求，这道题目就变得棘手了。 此题最常见也是最经典的解法是使用异或运算，这是一个很有技巧的方法，涉及到异或运算的性质，如果你不了解异或运算，那不妨参考下使用分治算法的解法。毕竟相比之下，分治的思想更深入人心。

//伪代码
FIND-SINGLE-NUMBER(A,low,high)
1 while (low < hight)
2   k = PARTITION(A,low,high)
3   if (k-low) mod 2 == 1
4 	  high = k-1
5   else low = k
6 return A[low]

算法的核心在于第三行的PARTITION, 这里的PARTITION其实就是快排算法的第一步，每次在A[low]和A[high]之间随机选取一个值作为中心值，通过$O(N)$复杂的PARTITION，将A分为左右两个部分，左边部分严格小于中心值，右边部分大于等于中心值；对于分割完毕的两部分，落单的值一定在元素个数为奇数的一边，所以对这一边进行递归操作，直到找出这个落单的值。因为采用了随机化的PARTITION可以证明该算法的时间复杂度为$O(N)$，在这里我们假设每次分割都近乎平均，那么算法运行时间的递归式为： $$ T(n) = T(n/2) + \Theta(n) $$ 根据主定理（算法导论第三版，定理4.1）可以解得 $$ T(n) = \Theta(n) $$ 为了更有力地说服这个算法时间复杂度是$ O(N) $的，特绘制异或算法与分治算法随n增大时的时间图像。 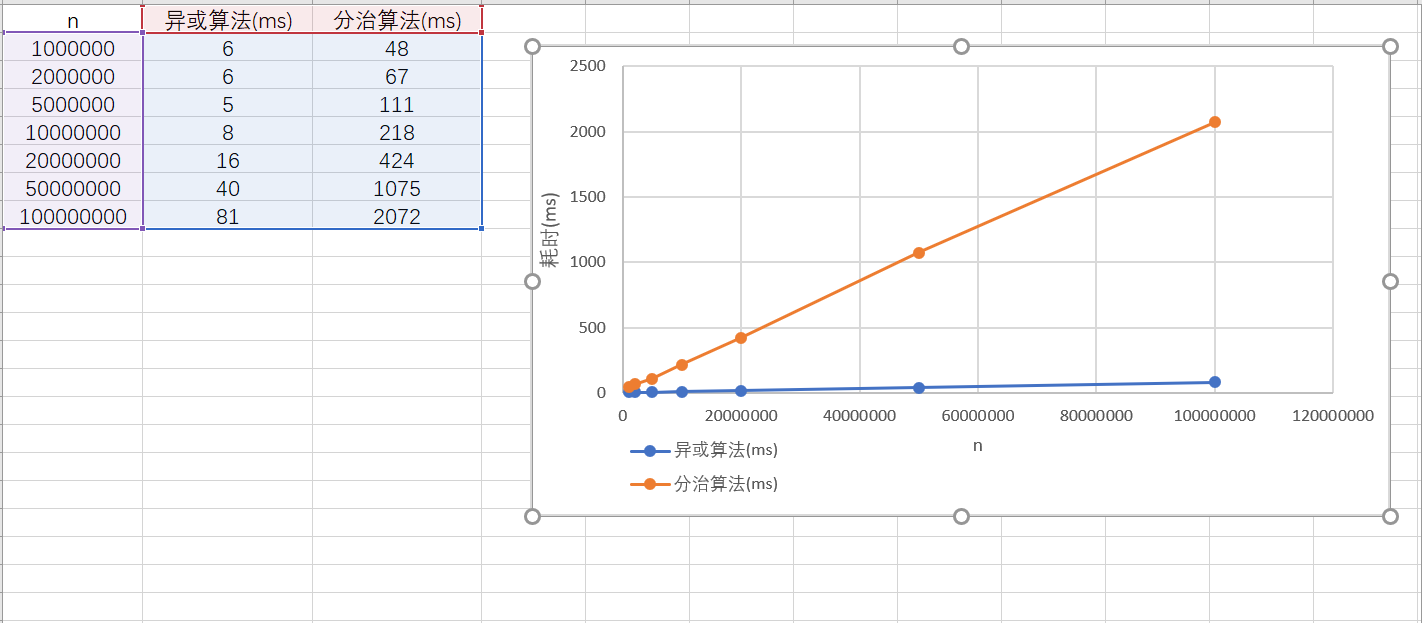Alert text 可以看到，相比于异或算法，分治算法的耗时确实更多，但的的确确是$ O(N) $的时间复杂度。

至于空间复杂度，在采用递归写法时，并不是一个常数，不过因为是尾递归，很容易改写成loop形式，此时的空间复杂度严格为常数。

Python代码：

import random
from typing import List

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        self.A = nums
        return self.foo(0, len(nums) - 1)

        
    def foo(self, low, high) -> int:
        while (low < high):
            k = self.partition(low, high)
            if (k - low) % 2 == 1:
                high = k - 1
            else:
                low = k
        return self.A[low]
        
    def partition(self, low, high):
        split=low - 1
        i = random.randint(low, high)
        self.A[i], self.A[high] = self.A[high], self.A[i]
        pivot=self.A[high]
        for i in range(low, high):
            if self.A[i] < pivot:
                split = split + 1
                self.A[split], self.A[i] = self.A[i], self.A[split]
        self.A[split + 1], self.A[high] = self.A[high], self.A[split + 1]
        return split+1